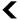Lindenmayer Systems: Unraveled
Introduction
Have you ever wondered how common objects in nature, such as trees, clouds, or snowflakes, get their shape? If so, you may either assume that it's a very complex process, or that there is no discernable "process" whatsoever. In reality, neither of these are true. The rules followed by such structures are deceptively simple, and their shapes are made complex through sheer persistence. In the example of trees, a simple rule such as, "Grow forward and branch to the left and right, creating two children" are repeated over, and over, and over again. We call this process iteration. For each iteration of the tree example, the number of "rule followers" increases, resulting in a more and more complex shape.
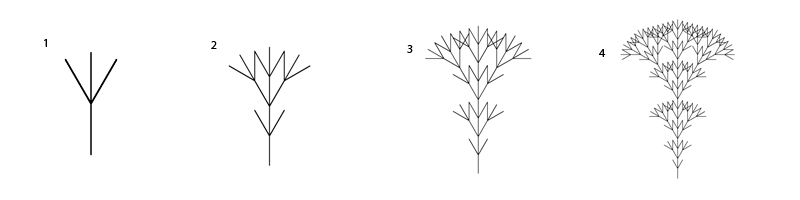
In 1968, a theoretical biologist and botanist from the University of Utrect named Aristid Lindenmayer noticed this trend, and succeeded in creating a simple procedure that allows the phenomenon to be easily simulated by the computer, and, moreover, easily understood by the human (depending on who you ask). The Lindenmayer System (also known as L-System) is a process by which a simple string (or series of characters), such as "F", is subjected to a Production Rule, such as: "F becomes F[<F][>F]F". If the same rule is applied a number of times, the string becomes exponentially longer, as each iteration begins with more Fs than the last. Amazing! But, it's not a tree.
Genotype and Phenotype
Correct. It's not a tree yet, but rather a blueprint for the creation of a tree. We call this concept the Genotype/Phenotype distinction, where the Genotype is the organic blueprint and the Phenotype is the resulting form. In other words:
Genotype: rules.
Phenotype: shape.
Practice Makes Perfect
This simulation illustrates the mathematical roots of natural phenomena such as plant growth (also mountains, clouds, etc.). Most naturally occurring phenomena are able to be represented by a simple formula repeated over and over again (e.g. a tree's branch closely resembles a smaller version of the tree as a whole).
Simply with this repetition a geometric shape becomes a fractal, a shape or surface comprised of smaller versions of itself. But that's enough about fractals for now.
To determine our system we have the "Production Rule", the settings for the replacement of certain characters in the L-String. L-Systems use a simple set of rules very much like Wolfram's Rule, using lines instead of blocks. Wofram's Rules uses its three "parents" to determine the color of the child. L-systems determine angle and and line length from a single parent.
Click the link below to go to our L-String generator. Don't worry! We will walk you through the basic functions of the program. Should you hunger for additional wisdom, feel free to continue reading. Alternatively, play with our simulation and continue to read simultaneously! The choice is yours.
>>>> Try it out! <<<<
The drawing program that our L-String Generator uses reads each of the characters in the L-String one by one, and carries out the simple instructions contained in each character. Here is a demonstration of how our example string; "F[<F][>F]F" would be drawn:
Creating the Phenotype
Now we're going to go into greater detail as to how the L-String (the series of characters that is our would-be tree, or other organic shape) is generated. Normally, we are going to begin with a simple "F". This stands for "forward", and will result in a single straight line if it is drawn. This is not a very exciting tree, and yet it is the basic root that all of our trees will extend from. Our Production Rule is the pattern that orchestrates the ultimate shape of the figure to be drawn. We will use "F => F[<F][>F]F" for this example. Now, we will iterate through the L-String a total of 3 times, and each time we will replace every F in the string with F[<F][>F]F. Since the production rule adds more Fs to the string during each iteration, the string will get longer and longer.
| Iterations | L-String |
| 0 | F |
| 1 | F[<F][>F]F |
| 2 | F[<F][>F]F[<F[<F][>F]F][>F[<F][>F]F]F[<F][>F]F |
| 3 | F[<F][>F]F[<F[<F][>F]F][>F[<F][>F]F]F[<F][>F]F[<F[<F] |
Crazy.
As you can see, the L-String grows more and more rapidly with each iteration. The L-String, or Genotype, we have after 3rd iteration contains instructions for drawing a fairly complex tree, or Phenotype.
Creating the Genotype from the Phenotype
Now, you might be wondering what all of those different characters mean. In fact, they are directions to be used by a drawing program! Their individual meanings are as follows:
| F | Draw forward. |
| < | Rotate to the left. |
| > | Rotate to the right. |
| [ | Create a new branch for drawing. |
| ] | Return to the previous branch. |
Think of the starting line as a seed, containing all the information to grow into a large intricate tree. This seed is minuscule and does not contain an entire tree, but manages to determine growth of an entire tree. This seed is called the genotype (i.e. sum total of genes transmitted from parents to offspring). Our genotype in the simulation is the rule, the rule is passed on to future generations, and creates the resulting system.
The tree and all of its branches is called the phenotype. Essentially the phenotype is the result, determined by the genotype, along with a few other factors (e.g. in nature the surrounding environment has a drastic effect on phenotype).
Identical twins, for example have the exact same genotype, they begin at the very same point. The genotype, determines a lot of their biology, but they still end up with distinct phenotypes (i.e. they look slightly different). They are not exactly identical, most people can even tell the difference between identical twins after knowing them a short while.
Genotype is the rule governing how something is created, and these simple guidelines create complex objects and beings. The phenotype can vary greatly but is still controlled by the genotype.
Fractals
Using our rule to determine the shape over and over again results in a fractal, as said above, a shape or surface comprised of smaller versions of itself. When a shape or surface is comprised of successive subdivisions of itself is is referred to as self-similarity, the parts of an object resemble the whole of the object. Similar to tree branches growing smaller branches which, in turn, grow even smaller branches
More on Fractals:
The following TED talk discusses exploration of the undiscovered worlds at the top of California redwood trees. It also goes on to briefly discuss how redwoods branch off into fractal trees of themselves. The trees do not only have branches, but upon those branches grow smaller trees that are essentially scaled down replicas of the large tree. This video has more about nature and less about math. (Start video at about 8:00 to skip to fractal discussion). Richard Preston on the Giant Trees
If fractals are your thing, you can watch this NOVA documentary on fractals, FOR FREE. NOVA Fractals